نرى المكان متصلا وندرك الزمان على نفس النحو؛
ولكن إذا صحت النظرية الغريبة حول الثقالة الكمومية العروية،
فإن الزمان والمكان هما في واقع الأمر مكونَان من قطع متفردة.
قبل ما يزيد على نحو مئة سنة كان معظم الناس ومعهم معظم العلميين يظنون أن المادة متصلة. ومع أن بعض الفلاسفة والعلميين قد تكهنوا منذ قديم الزمن بتكون المادة من ذرات دقيقة نصل إليها إذا ما قسمت المادة إلى أجزاء صغيرة بما فيه الكفاية، فقد تناقص عدد من كان يعتقد بإمكانية إقامة الدليل على ذلك. ولكننا اليوم نستوعب وجود ذرات فردية وندرس الجسيمات التي تتكون منها. ولم يعد أحد يستغرب تكوُّن المادة من حبيبات.
في العقود الأخيرة، تساءل الفيزيائيون والرياضياتيون عما إذا كان الفضاء أيضا مؤلفا كالمادة من قطع متفردة. هل الفضاء متصل كما تعلمنا في المدارس أو أنه أشبه بقطعة من القماش محبوكة من ألياف صغيرة منفصلة؟ أتُرى إذا استطعنا استكشاف قياس الأجسام البالغة الصغر، فهل سنرى «ذرات» يستحيل اختزالها أو تجزئتها إلى ما هو أصغر منها؟ وماذا عن الزمان: هل تتغير الطبيعة على نحو متصل أو أن الكون يتطور بتسلسلٍ من المراحل الدقيقة جدا وهو في ذلك أشبه ما يكون بحاسوب رقمي؟
شهدت السنوات ال16 الماضية تقدما كبيرا في هذه الموضوعات، إذ تتنبأ نظرية تحمل اسما غريبا هو «الثقالة الكمومية العروية»(1) بأن الفضاء والزمان مكونان من أجزاء متفردة. وتكشف لنا الحسابات المجراة في إطار هذه النظرية عن صورة بسيطة وجميلة في آن واحد. فقد عمقت النظرية فهمنا لظواهر محيرة ترتبط بالثقوب السوداء وبالانفجار الأعظم. وأفضل ما في الأمر أن هذه النظرية قابلة للاختبار، وتتنبأ بتجارب يمكن إجراؤها في المستقبل القريب تتيح الكشف عن ذرات الفضاء في حال وجودها.
ذرات المكان والزمان: نظرة إجمالية/ الزمكان الكمومي(**)
|
▪ لفهم بنية الفضاء في السلالم البالغة الصغر، علينا التوجه نحو نظرية كمومية للثقالة. ويتأتى تدخل الثقالة في هذا الموضوع من نظرية النسبية العامة لآينشتاين التي تبين أن الثقالة ناتجة من تشوه الزمان والمكان. ▪ إن التوفيق المتأني بين المبادئ الأساسية للميكانيك الكمومي والنسبية العامة هو الذي قاد الفيزيائيين لوضع نظرية «الثقالة الكمومية العروية». ويبدو أن الحالات الكمومية المسموح بها للفضاء في هذه النظرية مرتبطة بمخططات مكونة من خطوط ونقاط تسمى شبكات السپين. ويقابل الزمكان الكمومي مخططات مماثلة تسمى زبد السپين. ▪ تتنبأ الثقالة الكمومية العروية بأن الفضاء مكون من قطع منفصلة، حجم أصغرها نحو طول پلانك مكعب، أي 99-10 سم3. ويجري الزمن بدقات متفردة هي نحو 43-10 ثانية. ويمكن رؤية المفاعيل الناتجة من هذه البنية المتفردة (المتقطعة) في تجارب تجرى في المستقبل القريب. |
الكمات(***)
لقد قمت وزملائي بتطوير نظرية الثقالة الكمومية العروية في وقت كنا نتصارع فيه مع مسألة مهمة مطروحة في الفيزياء منذ زمن طويل: هل يمكن وضع نظرية كمومية للثقالة؟ ولشرح أهمية هذه المسألة ـ وعلاقتها بحبيبات الفضاء والزمان ـ يجب أن أتحدث قليلا عن النظرية الكمومية وعن نظرية الثقالة theory of gravity.
لقد صيغت النظرية الكمومية في الربع الأول من القرن العشرين وارتبطت صياغتها ارتباطا وثيقا بالبرهنة على أن المادة تتكون من ذرات. فمعادلات الميكانيك الكمومي تؤدي إلى ظهور بعض القيم، مثل طاقة الذرة على سبيل المثال، على شكل وحدات متقطعة محددة. وقد نجحت النظرية الكمومية في التنبؤ بخواص الذرات وسلوكها، وكذا بخواص وسلوك الجسيمات الأولية والقوى المكونة لها. ولم يحدث في تاريخ العلوم أن حققت نظرية ما نجاحا أعظم مما حققته النظرية الكمومية، فعليها يقوم فهمنا للكيمياء وللفيزياء الذرية وما تحت الذرية وللإلكترونيات وحتى للبيولوجيا
وفي نفس الفترة التي صيغ فيها الميكانيك الكمومي طرح آينشتاين نظريته العامة في النسبية وهي نظرية الثقالة. وتظهر قوة التثاقل في نظريته بسبب انحناء المكان والزمان المكونين معا «للزمكان»(2) الناتج من وجود المادة. ولتقريب الصورة للأذهان، يمكننا مقارنة ذلك بكرة بولينگ موضوعة على صفيحة مطاطية ومعها كرة من المرمر تتدحرج بالقرب منها. يمكن تمثيل الشمس والأرض بالكرتين والصفيحة بالفضاء. تتسبب كرة البولينگ بتضاريس عميقة في الصفيحة المطاطية ويؤدي انحدار التضريس إلى انعطاف الكرة المرمرية نحو الكرة الأكبر وكأنها قد دفعت في هذا الاتجاه بفعل قوة ما (الثقالة). وعلى نفس النحو تشوه أي قطعة من المادة أو أي تجمع للطاقة هندسة الزمكان مسببة انعطاف الجسيمات الأخرى والأشعة الضوئية نحوها وهي الظاهرة التي نسميها الثقالة gravity.
عززت التجربةُ النظريةَ الكمومية ونظرية النسبية العامة لآينشتاين، كلا على حدة بشكل مدهش. إلا أنه لم تجر أي تجربة مفاعيل effects مهمة تتنبأ بها كل من النظريتين. ويُردّ ذلك إلى أن المفاعيل الكمومية تبرز أقصى ما يكون في الأبعاد الصغيرة جدا، في حين تتطلب مفاعيل النسبية العامة كتلا كبيرة، وهكذا لا بد من ظروف غير عادية للجمع بين هذين الشرطين
وهناك إلى جانب هذه الثغرة في البيانات التجريبية مسألة عويصة تتعلق بالمفاهيم. فنظرية آينشتاين في النسبية العامة نظرية تقليدية تماما، أي إنها ليست كمومية. إلا أنه لكي تبقى الفيزياء علما متسقا لا بد من توحيد الميكانيك الكمومي والنسبية العامة. وتسمى هذه النظرية التي نبحث عنها منذ أمد طويل الثقالة الكمومية quantumgravity. ولما كانت النسبية العامة تتعامل مع هندسة الزمكان، فعلى نظرية الثقالة الكمومية أن تكون نظرية كمومية للزمكان.
لقد طور الفيزيائيون مجموعة من النهج والطرائق الرياضياتية لتحويل نظرية تقليدية إلى نظرية كمومية. وعمل العديد من الفيزيائيين النظريين والرياضياتيين على تطبيق هذه التقنيات على النسبية العامة. وكانت النتائج الأولى مثبطة؛ إذ يبدو أن الحسابات التي أجريت في الستينات والسبعينات من القرن العشرين أظهرت أن محاولة التوفيق بين النظرية الكمومية والنسبية العامة لن يكتب لها النجاح؛ ومن ثمّ كان لا بد من طرح متطلبات أساسية جديدة، مصادرات poslulates أو مبادئ لا تتضمنها النظرية الكمومية والنسبية العامة، أو جسيمات جديدة وحقول، أو نوع آخر من الكائنات الجديدة. ولعل إضافة من هذا القبيل أو لعل بنية رياضياتية جديدة تتيح لنا تطوير نظرية شبه كمومية تنجح في أن تكون النسبية العامة على وجه التقريب في النظام غير الكمومي. ثم إنه من الضروري أن تبقى هذه الإضافات الدخيلة في النظرية الإجمالية خافية عن التجارب كي لا تضر بالتنبؤات الناجحة للميكانيك الكمومي والنسبية العامة وألا تتبدى إلا في الظروف غير الاعتيادية، حيث يتوقع أن يكون لكلتا النظريتين مفاعيل كبيرة. وقد أجريت محاولات عديدة في هذه الاتجاهات أطلقت عليها أسماء مختلفة مثل نظرية اللاوي twistor، الهندسة غير التبديلية والثقالة الفائقة.
تتمتع إحدى المقاربات ـ وهي نظرية الأوتار ـ بشعبية كبيرة عند الفيزيائيين، وهي نظرية تفترض أن للفضاء ستة أو سبعة أبعاد ـ حتى الآن لم يُرصد أي منها على الإطلاق ـ إضافة إلى الأبعاد الثلاثة المعهودة. كما تتنبأ نظرية الأوتار بوجود عدد كبير من القوى والجسيمات الأولية الجديدة، إلا أنه لم يقم أي دليل بالرصد على وجودها حتى اليوم. ويعتقد بعض الباحثين أن نظرية الأوتار متضمنة في نظرية تسمى الأغشية (M–theory) [انظر: «النظرية التي كانت تسمى أوتارا»، مجلة العلوم، العدد 12(1998)، ص 34]، إلا أنه لا يتوافر حتى الآن أي تعريف دقيق لهذه النظرية المخمنة. وهكذا فإن كثيرا من الفيزيائيين والرياضياتيين مقتنعون بوجوب دراسة بدائل أخرى. ونظريتنا للثقالة الكمومية العروية هي أفضل البدائل المطورة.
ذرات المكان والزمان: ثغرة كبيرة(****)
في منتصف الثمانينات، قرر عدد منا إعادة تفحص مسألة إمكانية التوفيق بشكل متسق بين الميكانيك الكمومي والنسبية العامة باستعمال التقنيات المعتادة. وكان منهم <A. آشتكر> [وهو الآن في جامعة ولاية پنسلڤانيا] و<T. جاكوبسون> [من جامعة مريلاند] و<C. روڤلّي> [وهو الآن في جامعة البحر المتوسط بمرسيليا]. وكنا نعلم أن ثغرة مهمة أدت إلى النتائج السلبية في السبعينات: كانت جميع الحسابات التي أجريت تفترض أن هندسة الفضاء متصلة وملساء أيا كانت دقة فحصنا لهذا الفضاء، وذلك على غرار ما كان الناس يتصورون المادة قبل اكتشاف الذرة. وقد بين لنا بعض أساتذتنا والمشرفين علينا أنه لن يكون من الممكن الاعتماد على الحسابات القديمة لو تبين أن هذه الفرضية خاطئة.
وهكذا بدأنا بالبحث عن طريقة لإجراء الحسابات من دون أن نفترض أن الفضاء أملس ومتصل، وعمدنا بإصرار إلى عدم وضع أي فرضية تتجاوز ما اختُبر جيدا من مبادئ النسبية العامة والنظرية الكمومية. واحتفظنا على وجه الخصوص في صلب الحسابات التي أجريناها بمبدأين أساسيين في النسبية العامة.
المبدأ الأول، هو المبدأ المعروف باستقلال الخلفية(3). وهو ينص على عدم ثبات هندسة الزمكان، وأنها عوضا عن ذلك هندسة متطورة، أي إنها مقدار ديناميكي. ولكي نجد هذه الهندسة يجب حل بعض المعادلات المتضمنة لجميع مفاعيل المادة والطاقة. وتجدر الإشارة هنا إلى أن الأوتار في صياغتها الحالية لا تتمتع باستقلال الخلفية؛ فالمعادلات التي توصف الأوتار مبنية في زمكان تقليدي (أي غير كمومي) معين مسبقا.
والمبدأ الثاني، المعروف بالاسم المهيب: مبدأ لا تغيّر التماثل التفاضلي diffeomorphism invariance، هو وثيق الصلة باستقلال الخلفية. ويقتضي هذا المبدأ حرية الاختيار في النسبية العامة ـ على خلاف النظريات التي سبقتها ـ لأي جملة إحداثيات نستعملها في الزمكان لكتابة المعادلات. فما يُعرِّف نقطة ما في الزمكان هو فقط ما يحدث فيها فيزيائيا، وليس موقعها بالنسبة إلى جملة إحداثيات خاصة (لا توجد إحداثيات خاصة). إن هذا المبدأ بالغ القوة في النسبية العامة وذو أهمية أساسية فيها.
وبالتوفيق بدقة بين هذين المبدأين والتقنيات المعهودة في الميكانيك الكمومي، قمنا بتطوير لغة رياضياتية سمحت لنا بإجراء حسابات لتحديد ما إذا كان الفضاء متصلا أو متفردا (متقطعا)؛ وسعدنا بملاحظة أن هذه الحسابات كشفت أن الفضاء مكمم quantized. وهكذا وضعنا أسس نظريتنا للثقالة الكمومية العروية.
ونشير هنا إلى أن المصطلح «عروة» loop قد أُدخل لاحتواء الحسابات في النظرية على عرى صغيرة محددة في الزمكان.
الحالات الكمومية للحجم والمساحة(*****)
إن التنبؤ المركزي لنظرية الثقالة الكمومية العروية مرتبط بالحجوم والمساحات. لننظر إلى غلاف كروي يُعرّف الحدود B لمنطقة من الفضاء ذات حجم ما (أعلاه). حسب الفيزياء التقليدية (غير الكمومية) يمكن للحجم أن يقدر بأي عدد حقيقي موجب. إلا أن نظرية الثقالة الكمومية العروية تقول بوجود حد أدنى مطلق للحجم يغاير الصفر (نحو مكعب طول پلانك، أي99-10 سنتيمتر مكعب)، بحيث تقتصر مجموعة الحجوم الكبيرة على متتالية متقطعة من الأعداد. وبالمثل، يوجد حد أدنى للمساحات يغاير الصفر (نحو مربع طول پلانك، أي 66-10 سنتيمتر مربع) ومتتالية متقطعة من المساحات الكبيرة المسموح بها. ويشبه الطيف المتقطع للمساحات المسموح بها (في اليمين) وللحجوم (في الوسط) إلى حد كبير مستويات الطاقة الكمومية المتقطعة لذرة الهدروجين (في اليسار).
وللتبسيط، نرسم في كثير من الأحيان البيانيات ببعدين، إلا أنه من الأفضل تخيلها وهي تملأ الفضاء ذا الثلاثة أبعاد، لأن هذا ما تمثله فعلا. ثم إن هناك في التصور فخا يجب عدم الوقوع فيه؛ فالمخططات البيانية وعقدها ليست في أمكنة معينة من الفضاء، ولا يُعرّف المخطط إلا بكيفية ارتباط مكوناته معا وبصلتها بحدود معرّفة تماما مثل الحدودB مثلا. إن الفضاء المتصل ذا الثلاثة أبعاد الذي نتخيل أن البيانيات تحتله غير موجود ككائن منفصل. ولا وجود إلا للخطوط والعقد؛ إنها هي الفضاء؛ كما أن طريقة ارتباطها هي التي تُعرِّف هندسة الفضاء.
تسمى هذه البيانيات شبكات السپين spin networks لأن الأعداد الموضوعة عليها ترتبط بمقادير تسمى سپينات spins. لقد كان <R. پينروز> [من جامعة أكسفورد] أول من ارتأى في أوائل السبعينات إمكانية الدور الذي تؤديه شبكات السپين في نظريات الثقالة الكمومية. وكم كانت سعادتنا كبيرة عندما جاءت الحسابات الدقيقة التي قمنا بها عام 1994 مؤيدة لحدسه. ولعل من الضروري تنبيه القراء المعتادين على مخططات فايمان إلى أن شبكات السپين عندنا ليست مخططات فايمان، وذلك على الرغم من التشابه الظاهري بينهما. فمخططات فايمان تمثل التفاعلات بين الجسيمات المنتقلة من حالة كمومية إلى حالة أخرى، في حين أن مخططاتنا تمثل حالات كمومية ثابتة للحجوم والسطوح في الفضاء.
تمثل العقد والحافات (الأحرف) edges المنفردة مناطق من الفضاء صغيرة إلى أقصى حد: فالعقدة عادة هي مجسم حجمه نحو مكعب طول پلانك، والخط سطح مساحته نحو مربع طول پلانك. إلا أنه ما من شيء يحدد مبدئيا ضخامة شبكة سپين أو تعقيدها. فلو كان في مقدورنا رسم صورة مفصلة للحالة الكمومية ـ هندسة فضائها وقد انحنت وتشوهت بفعل تثاقل المجرات والثقوب السوداء وغيرها ـ لحصلنا على شبكة سپين عملاقة ومعقدة إلى حد لا يمكن تصوره، تحتوي على 10184 عقدة تقريبا.
وإذا كانت شبكات السپين تصف هندسة الفضاء، فماذا عن المادة والطاقة المحتواة في هذا الفضاء؟ وكيف نمثل الجسيمات والحقول التي تشغل مواقع في الفضاء ومناطق منه؟ تقابل الجسيمات، مثل الإلكترونات، نوعا من العقد أُضيفت إليها علامات أخرى لتمثيلها. وتُمثل الحقول، مثل الحقل الكهرمغنطيسي، بعلامات إضافية على المخططات البيانية. ونمثل الجسيمات والحقول المتحركة عبر الفضاء بهذه العلامات المتحركة في خطوط متفردة على البيانيات.
ذرات المكان والزمان: حركات وزبد(********)
لا تقتصر الحركة على الجسيمات والحقول؛ فتبعا للنسبية العامة، تتغير هندسة الفضاء مع الزمن. فمنعطفات الفضاء وانحناءاته تتغير عندما تتحرك المادة والطاقة وتمر الموجات عبر الفضاء على غرار التموجات على سطح بحيرة(10). تتمثل هذه السيرورات في نظرية الثقالة الكمومية العروية بتغيرات في البيانيات. وتجري في الزمان عبر سلسلة من «الحركات» تتغير فيها الصلات في البيانيات [انظر الشكل في الصفحة 81].
يقوم الفيزيائيون عند توصيفهم الظواهر حسب الميكانيك الكمومي بتقدير احتمالات السيرورات المختلفة. ونفعل الشيء نفسه عندما نطبق نظرية الثقالة الكمومية العروية لتوصيف الظواهر، سواء تحركت الجسيمات والحقول على شبكات السپين أو تطورت هندسة الفضاء نفسه مع مرور الزمن. وقد تمكن <Th. تيمان> [وهو من معهد پيرمِتر Perimeter للفيزياء النظرية في واترلّو، كندا] من اشتقاق احتمالات كمومية دقيقة لحركات شبكة السپين، وبهذا تكون النظرية قد حُدِّدت تماما، لدينا إجراءات معرَّفة بشكل جيد لتقدير احتمال أي سيرورة يمكن أن تحدث في عالم يخضع لقواعد نظريتنا. ويبقى علينا فقط القيام بالتقديرات وإعداد التنبؤات بما يمكننا أن نرصده تجريبيا في هذه التجربة أو تلك
إن نظريتي آينشتاين في النسبية الخاصة والعامة تدمجان المكان والزمان في كيان واحد يُعرف باسم الزمكانspacetime. وشبكات السپين، التي تمثل الفضاء في نظرية الثقالة الكمومية العروية توائم هذا المفهوم ليصبح ما نسميه «زبد» السپين(11). وتتضخم خطوط شبكات السپين عندما نضيف بعدا آخر ـ الزمن ـ لتصبح سطوحا ذات بعدين وتتضخم العقد لتصبح خطوطا. وتمثل الانتقالات في شبكات السپين (الحركات التي جئنا على مناقشتها) بعقد هي نقط التقاء الخطوط في الزبد. وقد اقترح العديد من الباحثين صورة زپد السپين هذه للزمكان، ومن بين هؤلاء <C. روڤيلّي>.
وفي نظرتنا للأشياء في الزمكان، فإن صورة خاطفة في لحظة معينة أشبه ما تكون بقطع شريحة من الزمكان، إلا أنه من الخطأ اعتبار هذه الشريحة وكأنها تتحرك بشكل متصل على غرار تدفق سلس للزمن. ذلك أن الزمان، مثله مثل الفضاء المعرّف بهندسة متفردة لشبكات السپين، معرف بسلسلة من الحركات المتميزة التي تعيد ترتيب الشبكة، وذلك كما يبين الشكل في الصفحة المقابلة. وهكذا يصبح الزمن متفردا أيضا. فالزمن لا يجري مثل النهر وإنما مثل دقات الساعة، وطول هذه «الدقات» هو نحو زمن پلانك: 43-10 ثانية. وبتدقيق أكثر، نشير إلى أن الزمن يتدفق في الكون بدقات عدد غير منته من الساعات ـ بمعنى أن في كل موضع من زبد السپين، حيث «يتحرك» الكمّ، ساعة تدق مرة واحدة عندما تقع في ذلك الموضع.
تنبؤات واختبارات(*********)
لقد عرضتُ الخطوط العريضة لما تقوله نظرية الثقالة الكمومية العروية حول المكان والزمان في نطاق سلم پلانك، إلا أننا لا نستطيع أن نتحقق من صحة هذه النظرية مباشرة وذلك بتفحص الزمكان في هذه الأبعاد لشدة صغرها. فكيف يمكننا والحال هذه اختبار النظرية؟ إن أحد الاختبارات المهمة هو معرفة ما إذا كان من الممكن اشتقاق النسبية العامة التقليدية كتقريب للثقالة الكمومية العروية. أو بعبارة أخرى، إذا كانت شبكات السپين شبيهة بخيوط حيكت لتصبح قطعة قماش، فإن هذه المعرفة مماثلة للتساؤل عما إذا كان يمكننا تقدير خواص المرونة الحقيقية لصفيحة من مادة ما انطلاقا من خواص آلاف الخيوط المكونة لها وأخذ القيمة الوسطية لها. وعلى نفس النحو، عندما نأخذ القيمة الوسطية من أجل أعداد كبيرة من أطوال پلانك، ترى هل تصف شبكات السپين هندسة الفضاء وتغيرها مع الزمن بشكل يتفق إلى حد ما مع «القماش الناعم» لنظرية آينشتاين التقليدية؟ إن هذه مسألة صعبة، إلا أن الباحثين حققوا حديثا تقدما في بعض الحالات؛ عندما تكون المواد في أوضاع معينة إن صح التعبير. وعلى سبيل المثال يمكن وصف الموجات التثاقلية الطويلة الموجة والمنتشرة في فضاء منبسط (لا انحناء فيه) كإثارات لحالات كمومية معينة توصفها نظرية الثقالة الكمومية العروية.
وهناك اختبار آخر مثمر هو النظر فيما تقوله نظرية الثقالة الكمومية العروية بشأن أحد الألغاز المطروحة منذ أمد طويل في فيزياء التثاقل والميكانيك الكمومي ألا وهو تيرموديناميك الثقوب السوداء، وعلى وجه الخصوص أنتروبيتها(12)، المرتبطة بالفوضى. وقد قام الفيزيائيون بحساب التنبؤات المتعلقة بتيرموديناميك الثقوب السوداء مستعملين نظرية تقريبية هجينة تُعالج فيها المادة معالجة كمومية، في حين لا يُعالج الزمكان كموميا. ويجب، والحالة هذه، أن يكون بمقدور نظرية كمومية كلية، مثل نظرية الثقالة الكمومية العروية، أن تطرح هذه التنبؤات. وتخصيصا، خلص <D .J. بيكنشتاين> في السبعينات من القرن العشرين، إلى أنه يجب أن تسند إلى الثقوب السوداء أنتروبية متناسبة مع مساحتها السطحية(13). وقد استنتج <S. هوكينگ> بعيد ذلك، أن الثقوب السوداء، والصغيرة منها على وجه الخصوص، يجب أن تصدر إشعاعات. وتعد هذه التنبؤات من أعظم نتائج الفيزياء النظرية في الثلاثين سنة الماضية(14).
وللقيام بالحسابات في نطاق نظرية الثقالة الكمومية العروية، نختار الحدود B لتكون أفق الحدث للثقب الأسود. وعندما نحلل أنتروبية الحالات الكمومية ذات الصلة نحصل بالضبط على تنبؤات بيكنشتاين. وعلى نفس النحو تقودنا النظرية من جديد إلى تنبؤ هوكينگ بإشعاع الثقب الأسود، بل تزودنا في واقع الأمر بتنبؤات جديدة تتعلق بالبنية الدقيقة لإشعاع هوكينگ؛ أي إنه لو حدث يوما ما أن رصد ثقب أسود مجهري الأبعاد لأمكن اختبار هذه التنبؤات بدراسة طيف الإشعاعات التي يصدرها. وقد يكون ذلك بعيد المنال لأننا لا نملك أي تقنية لصنع ثقب أسود سواء كان صغيرا أو كبيرا.
تنّشؤ الهندسة في الزمن(**********)
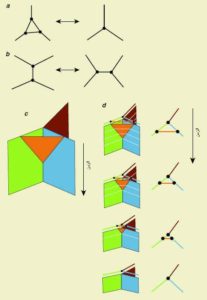
تتمثل التغيرات في شكل الفضاء ـ مثل تلك التي تحدث عندما تتحرك المادة والطاقة أو عندما تتدفق الموجات التثاقلية فيه ـ بإعادة ترتيب متفرد (متقطع) للأنساق، أو الحركات، في شبكة السپين. ففي a، تندمج زمرة مؤلفة من ثلاثة حجوم كمومية لتصبح حجما كموميا منفردا. كما أنه يمكن حدوث السيرورة المعاكسة. أما في b، فإن الحجمين يقسمان الفضاء ويتصلان بالحجوم الأخرى بطرق مختلفة. وإذا مثلناهما بكثيرات الوجوه، فإن كثيري الوجوه يندمجان عبر وجههما المشترك ثم يتفرقان كما تنفصل بلورة شطرت وفق مستو مختلف. وتحدث حركات شبكة السپين هذه عندما تقع تغيرات في هندسة الفضاء في الأبعاد الكبيرة، وتحدث كذلك في سلم پلانك دون انقطاع على شكل تأرجحات كمومية.
إن الطريقة الأخرى لتمثيل الحركات هي إضافة الزمن إلى شبكة السپين. ونسمي الحاصل زبد السپين spin foam c . تصبح خطوط شبكة السپين مستويات، وتصبح العقد خطوطا. وبأخذ شريحة عبر زبد السپين في زمن معين، يُنتج شبكة السپين، أما أخذ سلسلة من الشرائح في أزمان مختلفة فينتج لقطات شريط سينمائي يبين تطور شبكة السپين مع الزمن (d). إلا أنه يجب ملاحظة أن التطور الذي يبدو للوهلة الأولى مستمرا وأملس هو في واقع الأمر متقطع. تمثل جميع شبكات السپين التي تحتوي على الخط البرتقالي (اللقطات الأولى الثلاث المبينة) هندسة متطابقة تماما للفضاء. فليس لطول الخط البرتقالي أي أهمية ـ إن ما يهم في الهندسة هو كيفية اتصال الخطوط ببعضها والعدد الذي يسم كل خط لأن هذا هو الذي يعرف النسق الذي وضعت عليه كمّات الحجوم والسطوح كما يعرف مقاديرها. وهكذا تبقى الهندسة ثابتة في d خلال اللقطات الثلاث الأولى، مع 3 كمّات حجم و6 كمات مساحة سطح. ثم تتغير الهندسة بشكل متقطع لتصبح كمّ حجم واحد و3 كمات مساحة سطح، كما تبين ذلك اللقطة الأخيرة. وعلى هذا النحو، فإن الزمن المعرف بزبد السپين يتطور بحركات متقطعة مفاجئة وليس بتدفق مستمر.
ومع أن الحديث عن متتاليات كهذه مثل لقطات شريط سينمائي يساعد على تخيل ما يحدث، إلا أن الطريقة الأصح لفهم تطور الهندسة، هي النظر إلى هذه المتتاليات مثل دقات متقطعة لساعة. يظهر كمّ المساحة البرتقالي عند دقة ويختفي عند الدقة التي تليها؛ والواقع أن اختفاء كمّ المساحة البرتقالي هو الذي يعرف الدقة. والزمن الفاصل بين دقتين متتاليتين قريب من زمن پلانك، أي43-10 ثانية. لكن لا وجود للزمن بين دقتين؛ ولا وجود ل«بين» هنا تماما كما هي الحال في الماء، فلا وجود له بين جزيئين متجاورين من الماء.
مجلة العلوم (أغسطس – سبتمبر2004 / المجلد 20)
مراجع للاستزادة
Three Roads to Quantum Gravity. Lee Smolin. Basic Books, 2001.
The Quantum of Area? John Baez in Nature, Vol. 421, pages 702-703; February 2003.
How Far Are We from the Quantum Theory of Gravity? Lee Smolin. March 2003. Preprint available at http:.//arxiv.org/hep-th/03031H5
Welcome to Quantum Gravity. Special section. Physics World, Vol. 16, No. 11, pages 27-50; November 2003.
Loop Quantum Gravity. Lee Smolin. Online at
www.edge.org/3ni_cukure/smolin03/smolin03_indexhtml
Scientific American, January 2004
(*) ATOMS OF SPACE AND TIME
(**) Overview/ Quantum Spacetime
(***) Quanta
(****) A Big Loophole
(*****) Quantum States of Volume and Area
(******) Visualizing Quantum States of Volume
(*******) Spin Networks
(********) Moves and Foams
(*********)Predictions and Tests
(**********) Evolution of Geometry in Time
(***********) An Experimental Test
(1) loop quantum gravity
(2) space-time زمكان، وهذه نحت من زمان ومكان. (التحرير)
(3) background indepedence
(4) event horizon
(5) [انظر: «الأخبار العلمية» في هذا العدد].(التحرير)
(6) Planch length
(7)ج: كمّ quantum
(8) polyhedra
(9) ج: مخطط بياني، أو اختصارا بياني وجمعها بيانيات، وذلك لتمييزها عن بيانات data.
(10) [انظر:” Ripples in Space and Time”,
by W. Wayt Gibbs; Scientific American, April 2002].
(11)spin foam
(12) entropy
(13) [انظر: “Information in a Holographic Universe,
by J. D. Bekenstein; Scientific American, August 2003].
(14) [انظر: «الأخبار العلمية» في هذا العدد]. (التحرير)
(15) discreteness
(16) big bounce
(17)constant the cosmological
(18) discontinous
(19) [انظر: “The Quintessential Universe”,
by Jeremiah P. Ostriker – Paul J. Steinhardt;
Scientific American, January 2001]